OF MEME REPLICATION
by Aaron Lynch
Notice: For a more current and comprehensive treatment,
see the 2001 paper Units, Events, and Dynamics in the
Evolutionary Epidemiology of Ideas
at http://www.thoughtcontagion.com/UED.htm.
Non-scientists: The following paper is extremely technical.
For an explanation of memetics broadly accessible
to non-scientists,
see articles and a book chapter featured on the
Thought
Contagion Science Page
This paper is a re-titled revision of a 1991 paper.
ABSTRACT
An evolutionary recursive replicator theory of mental/brain information is presented. Noting that all replicator theories rest at least tacitly upon the fundamental notions of causation and of calling two or more entities "the same" with respect to an abstraction, the concept is rendered explicit in defining the terms "mmemon" and "meme." A symbolic calculus of mnemon conjugations and replication events follows. Differential equations are developed for meme host population versus time in a two-meme system, modeling the dynamics whereby events at the individual level give rise to trends at the population level. This lays a foundation for computerized simulations and the falsification or verification of specific memetic hypotheses. Mechanisms of creativity as a population phenomenon are examined, with the memetic perspective yielding a novel explanation for the temporal clustering of independent co-creations. Creation and propagation are integrated into a theory of evolution by variation and natural selection of memes.
KEYWORDS: Meme, mnemon, evolution, replication, causation, abstraction,
memory, idea, event, population psychology, population memetics.
This article was previously published (less some revisions) in Journal
of Ideas, January 1991.
The Journal of Ideas, an all-memetics print journal, ceased publication
after its first year for lack of funding.
A strictly online Journal
of Memetics has been established in 1997.
No endorsement or criticism of specific articles in JOM is implied
by this link.
Introduction
In memetics, organic evolution, biological contagions, and computer viruses serve as metaphors for the spread of beliefs. In principle, however, someone could have offered a treatise on the replication, proliferation, and evolution of beliefs long before Darwin's work on evolution, Pasteur's work on microbiology, Mendel's work on genetics, or Turing's work on automata. Indeed, that treatise might even have afforded metaphors to these other disciplines had it appeared by the early 1800's. On this planet, though, the history of science has its social and information fields drawing metaphors from biology rather than the other way around.
Like all metaphors, the ones linking beliefs to organic and software contagions have their limitations. Metaphors make powerful literary and explanatory devices, and can render a potentially dry and abstruse book interesting and readable. But relying too heavily on them can lead to bad science. It makes sense, then, to recast the core concepts of Thought Contagion theory in language that does not depend on analogies to the biological or computer sciences. The analysis is drier, but it does formally illuminate some ways that thought contagions depart from strict analogy to other replicators. It also provides some philosophy of science behind memetics theory while lending a stronger platform for mathematical and empirical investigations.
Units of Memory Replication
Defining the "self-replicating" idea is as critical to memetic evolution theory as defining the units of heredity was to genetic evolution theory. The gene's definition developed as empirical investigations led away from the hypothesized inheritance of acquired characteristics to the biochemical sequencing of DNA strands. The universal code of these strands constituted a natural "language" upon which scientists based their own more symbolic and abstract language. The biologists' terminology is thus a metalanguage to the more concrete language of nucleotide sequences.
Yet for the evolution of ideas, no equally understood concrete language has been discovered. Science has achieved no direct observation of the neural encoding of ideas, which might have provided us a precise language for discussing ideas. Indeed, even if we knew in principle how to express ideas in terms of neurons, synapses, etc., the description would likely be prohibitively complex. So instead of language based on a concrete mechanism of information storage, we must settle for an abstract representation of the information stored. Thus, memory abstractions form the basis for Memetic Evolution theory.
Most people use abstract representations of memory content on a daily basis to discuss ideas. When we say that two people have "the same" idea, we do not use "sameness" to mean equality in every concrete detail, or else we could never correctly say that two people have the same idea. We mean that one person's idea has at very least one quality in common with the other's idea. Perceiving two people to have "the same" idea involves abstracting out a set of common qualities. So saying that two people's ideas are "the same" only means that they are in some way "of the same kind," or congeners.
This ability to say that two people have the same idea lies at the foundation of the notion of a "self-replicated idea." When an idea "self- replicates," it acts to produce or preserve ideas that we call "the same idea." The resultant ideas can for now be called "self-replicated" ideas. To be a self-replicated idea means not only to have resulted from a given idea, but also to be "the same" as that idea. Specifically, it means meeting some abstract, observer-defined criterion for sameness.
Self-replicated ideas are not all exact replicas of their originals. A wide range of ideas may result from each self-propagating original. An observer just selectively lumps these proliferated ideas along with their original(s) into a set, using an abstract inclusion criterion.
As an example, the belief that "abortion is wrong" has a wide range of different meanings to different people. The range includes people who regard abortion as merely unethical to those who see the "morning after pill" as a high felony. So, although the belief varies greatly from person to person, its occurrences are all "the same" in the limited respect of fitting the above definition. Encountering a range of such beliefs in actual people, one simply "abstracts out" a common element running through all of them. On writing out a definition of this abstracted common element, or sameness criterion, one can proceed to use it for natural selection reasoning.
The abstraction could just as well be more general or more specific, depending upon our interests. A memeticist might, for instance, choose the more specific belief "abortion is a mortal sin." Then many quantitative variables involved in its natural selection would differ from those associated with the broader definition. First, the more restrictive definition would almost certainly identify a smaller host population. Second, when the hosts communicate their belief to friends and family, a likely smaller fraction of listeners will become new hosts per exposure. This is because any listeners who go away newly convinced that abortion is merely unethical no longer count as new hosts. Becoming a host of the more restrictively defined belief takes more of what Dawkins calls copying fidelity. Third, once a host, one may do less "ideological wavering" before being counted as a drop out. That is, remaining the host of a more restrictively defined belief takes more preservation fidelity. So changing an idea's definition can make a big difference in the evolutionary phenomena identified with it.
Other Propagating Items
Many psychological phenomena other than ideas can be observed to self- replicate. These include habits, attitudes, class identities, cognitive associations, education, emotional dispositions, addictions, and even neurotic and psychotic symptoms.
All these traits may be broadly classified as human memory content. This category is more general than the word "idea" or even "memory" usually connote. This broad technical meaning of "memory," as defined in Webster's New Collegiate Dictionary, is "the store of things learned and retained from an organism's activity or experience as evidenced by modification of structure or behavior or by recall and recognition." Thus, the principle abstractions manipulated with memetics theory are memory abstractions, or mnemons.
Mnemons do not include inanimate propagating items such as chain letters, Bibles, etc. The focus on mnemons expresses the opinion that propagating mental phenomena are central to the spreading of most human artifacts and actions that one might view as self-propagating. Using mnemons also helps to standardize the measurement of propagation in terms of a host count. Thus, a chain letter or the copying machine duplicating it do not count as hosts, but the person photocopying the letter does.
This restriction roughly parallels the definition given to the term gene in biology. There, the term generally refers to information as encoded in nucleic acids. A printout containing thousands of T's, A's, G's, and C's may contain the same information, but does not strictly count as a gene in its own right. Neither does a protein specified by the gene, even though it, too, can hold the same information.
Other work does address non-mnemon replicators as well as population memory items that do not exist in any one individual, but rather, in systems of individuals.
If a mnemon resides very redundantly in someone's brain, that person still counts as only one host and one mnemon instantiation. The number of duplicates of a memory item in one brain is not currently measurable, so it escapes further treatment in this article.
Representing Mnemons Symbolically
Mnemons can be represented conveniently with symbols such as "A," "B," etc. Thus, we can call the hell belief mnemon A, the imminent doomsday belief mnemon B, and a combination of mnemons such as the hell/imminent doomsday combination "A*B." The "*" indicates that A and B are instantiated in the same host. Extending this concept, one can represent a whole system of mnemons as "A*B*C*..."
Symbolic expressions can also represent mnemon replication much the way chemists represent chemical reactions. Thus, the hell belief's proselytic propagation may be represented as A + ~A --> 2A. This expression is read as "Host of A together with a non-host of A yields two hosts of A." (The two hosts on the arrow's right are the same two people as on the left side, one of whom is converted from non-host to host status. Note also the generalized use of the word "proselytic.") The mnemons on the left side of the arrow are called the input mnemons, and those on the right, the output mnemons.
A transition such as A + ~A --> 2A, realized in particular people at a particular time, constitutes an evolutionary event in the ideosphere. Other evolutionary events include: A --> ~A (host of A drops out), ~A --> A (non- host independently forms A), A --> 0A (host of A dies), and 2A --> 2A + ~A (two hosts of A have a baby non-host of A).
Even multi-stage evolutionary events are handily represented by this
system. For instance, the childbirth event can be extended to the form
2A --> 2A + ~A --> 3A. (Two hosts of A have a baby and then spread their
A-mnemon to the child.) A more complicated possibility is
A + ~A --> A + 2~A --> 2A + ~A. (Host plus non-host of A have a baby
who later adopts the A-mnemon from the A-host parent.)
Some multi-stage events are best represented by two or more diagrams.
For example, if two hosts of A have a baby non-host and then have their
local Sunday school teacher instill the A-mnemon in the child, one would
represent it as two
events: 2A --> 2A + ~A (the birth) and 3A + ~A --> 4A (the catechism).
In the second event, the three input
A-hosts are the teacher and the two parents (who select the teacher).
Representing the events separately (instead of
as 3A --> 3A + ~A --> 4A) conveys with greater accuracy that the teacher's
conceptual contributions occurred only after the birth. Many two stage
events pertain to the parental replication because that mode generally
involves both having and training children.
Complementary Mnemons
Treating ~A as a mnemon along with A may seem rather strange. People labeled "~A" may be called ~A-mnemon hosts or A-mnemon non-hosts. (A and ~A are called complements of each other.) But can a person's lack of the A-mnemon justifiably be called a mnemon itself? It sounds like saying that nothing is something.
The meaning of the term "mnemon" provides an answer to this question. Mnemons are merely memory abstractions. As such, a negatively defined mnemon--which only states what a person does not have--is just as much of a memory abstraction as is a positively defined mnemon. Saying that someone "has" or "hosts" a mnemon like ~A, really means that the person satisfies the definition of the particular memory abstraction (i.e., the person instantiates the abstraction). It is exactly what we mean when we say that a person "hosts" a positively defined mnemon.
Negatively defined mnemons can also self-propagate, as with the childbirth event 2~A --> 3~A, where A is a knowledge-of-birth-control mnemon. (One might define this mnemon functionally as knowing how to use at least one of some particular list of methods.) Because ~A-hosts have fewer birth control options than do A-hosts, the ~A-mnemon enjoys a greater quantity-type parental replication advantage. Nonetheless, the A- mnemon has done very well in modern times, largely since people can be taught about birth control far more easily than they can be made to forget about it. Since proselytizing it is impossible, the ~A mnemon depends on parental events that occur just a few times per generation. The A-mnemon, on the other hand, proliferates proselytically for various reasons, including both the sexual and humanitarian motives of its hosts. So both A and ~A self-propagate, leaving us no choice but to consider the propagation of both a positively defined mnemon and a negatively defined mnemon in investigating this example.
Incidentally, ~A's parental propagation does not conform to the tendency, mentioned earlier, for the parental replication mode to involve multi-stage evolutionary events. People are born with ~A, so that giving birth and "imparting" the mnemon are actually the same event. After birth, the parents can at most act to preserve ~A in their child.
Mnemon Combinations
Multi-mnemon events describe phenomena--like idea alteration or recombination--too complex to represent with one complementary mnemon pair alone. For example, forming the hell/imminent doomsday pair by recombination can be represented as A*~B + ~A*B --> A*~B + A*B, where A = the hell mnemon and B = "doomsday is imminent." In this event, a person with only the A-mnemon spreads it to someone with only B, so that the latter person now has both A and B. This new combination may very well spark some new ideas in the A*B-host. He might experience the event A*B*~C --> A*B*C, where C is the belief that "I must urgently spread my faith to others because it may soon be too late!" Consequently, he may repeatedly play the leading role in the event A*B*C + ~A*~B*~C --> 2A*B*C. A, B, and C act cooperatively here to bring about their collective propagation.
Mnemons A, B, and C are all rather "unpleasant" ideas, so it does not seem too surprising to find them propagating cooperatively. Yet in the real world, these three propagate cooperatively with a very "pleasant" mnemon D: "Love your neighbor as yourself." A*B*C*~D motivates its hosts to spread their faith only to those "unbelievers" that they really care to see saved from hell. In marked contrast, A*B*C*D hosts should be motivated to spread their faith to any unbelievers they should happen to meet. So the combination of mnemons probably spreads more vigorously due to the inclusion of the D-mnemon.
When mnemons propagate synergistically as do A, B, C, and D, they may propagate primarily as a set rather than individually. In such cases, the set may be usefully defined as one mnemon. Thus, one might define E = A*B*C*D and consider E to be a stable, propagating mnemon in its own right. This approach can sometimes be used to study very large ideological systems, such as religious and political doctrines, by treating them as single (but lengthily defined) memory abstractions. The propagation events, however, often contain many intricate stages.
Moreover, in specifying mnemon "X" by an equation like X = A*B*C*..., one runs the risk of specifying so many "little" constituent mnemons that no one person ever actually has all of them. Mnemon X would then be a useless abstraction. Abstract evolution theory allows its own hosts enormous freedom to specify their preferred abstractions, yet the theory does not guarantee all those abstractions to be useful in studying the real world.
Competing Mnemons
Competition rather than cooperation characterizes many interacting mnemons. A mnemon competes against its complement in the knowledge-of- birth-control case mentioned above. The two complementary mnemons--each "armed" with distinct replication advantages--"struggle" for host population.
Yet more heated than this competition--at least in some nations--is the competition between moral stances on the subject. Personal morality, after all, has a greater bearing on an adult's use or non-use of various methods in a society where birth control information is highly available. Moreover, morality strongly influences the parental decision to actively instruct children on birth control or to actively obstruct their learning on the subject.
So in addition to the knowledge-of-birth-control mnemon (mnemon A),
we should also consider mnemon B, the moral acceptance of practicing birth
control, and mnemon C, the belief that birth control is immoral. Here people
are born with the ~A*~B*~C combination, but they never end up simultaneously
having B and C later on. This is because B and C are contrary, as distinct
from complementary mnemons. Since they are mutually exclusive, they are
destined to have a competitive rather than a cooperative relationship in
the ideosphere. The B mnemon is favored by a high occurrence of the proselytic
event
B + ~B --> 2B, while C is favored by a high rate of the parental event
2C --> 2C + ~C --> 3C. B benefits proselytically due to the same kind of
sexual and humanitarian motives for spreading it as does the A mnemon.
C spreads "parentally" because people who believe that birth control is
immoral do tend to have more children. Economic motives for spreading and
adopting the two mnemons also exist, and vary among situations. Additionally,
the drop out rate of children raised as C-hosts varies with population
homogeneity, media exposure to B, etc.
Homogenic and Heterogenic Events
The birth control example as treated so far fails to acknowledge people's ability to independently invent or re-invent moral decisions on their own. People are portrayed as acquiring mnemons only by copying them from others or by being born with them (as in the case of negatively defined mnemons).
To remedy this omission, consider the cases of two students who learn about birth control methods and then make moral judgments based on what they have learned. The first decides the practice is morally acceptable (A*~B --> A*B). The second decides it is not (A*~C --> A*C). Of course, people can make moral judgments without knowing birth control methods, but in this case our two hypothetical students judged only upon gaining the knowledge.
So one mnemon precipitates the formation of another mnemon, instead of just a new copy of itself. Mnemons that do this are called heterogenic (abbreviated as HeG), or "other-forming." The corresponding events, such as A*~B --> A*B, are called heterogenic events. The other type of event, which produces copies of input mnemons, is appropriately called a homogenic (abbreviated HoG), or "same-forming" event. The input mnemon that gets copied is called a homogenic mnemon.
Mnemon event symbolism and vocabulary now acknowledge that people can
form opinions for themselves without simply copying others' ideas. Yet
on many topics, people copy more ideas than they either originate or "re-
originate." For many beliefs, such as the birth control taboo, homogenic
formation far outweighs heterogenic formation in its overall occurrence
rate. The reason is that HoG events have the tendency toward self iteration
while HeG events do not. Generally speaking, anything that increases the
availability of the input mnemons will increase the expected frequency
of the event. Homogenic events, such
as 2A --> 2A + ~A --> 3A, increase their own input mnemons. So they
often tend to increase their own likelihood of recurring.
In contrast, HeG events, such as A*~B --> A*B, actually decrease their own input mnemons by one with each occurrence. This tends to decrease the HeG event's recurrence rate. Yet the independent thinker can pass the new, heteroderivative (HeD) mnemon along, resulting in homogenically formed, or homoderivative (HoD) mnemons. So after the first few heterogenic formations of the birth control taboo, the formation of new taboo hosts tends to become rapidly predominated by homogenic events.
One mnemon whose host population accumulates many members through both homogenesis and heterogenesis is the belief that "It is best not to go to church on Sunday." Many of its hosts received it (homogenically) from parents or friends who already had the idea. This makes their mnemons HoD (homoderivative).
However, many people got the idea because as children their parents made them go to church every Sunday, even when they did not feel like going. The resulting aversive experiences often lead the children to conclude that it is best not to go to church on Sunday. Ironically, their belief results from their parents' strict adherence to exactly the opposite belief. The pro-churchgoing mnemon influences some parents to generate something radically different in some of their children. So those parents' mnemon is HeG while the children's mnemon is HeD. Any parent who raises some children to be church going and some to be church avoiding has a churchgoing mnemon that is both homogenic and heterogenic.
The concepts of replicator evolution and epidemiology directly pertain only to the HoD sector of a mnemon's host population. In this sector, we can properly refer to mnemons as the "units of imitation" discussed by Dawkins. This allows a very restricted denotation in which a meme is defined as a homoderivative mnemon. The definition of a particular meme contains an abstract sameness criterion like the ones defining mnemons, but also includes a criterion of causality, namely, that it is homoderivative. So each meme has a corresponding mnemon: the memory abstraction defined without reference to HoD causation.
Although the church-avoiding mnemon does not occur primarily as a meme, one can still understand its proliferation in terms of memes. Simply divide the hosts into two groups: hosts of the church avoiding meme and dropouts of the church going meme (meme and meme-derived mnemon hosts). The first group can be studied directly as meme hosts. The second group's growth rate can be studied as a function of the church-going meme frequency. So the study of meme proliferation can be valuable to understanding the growth or decline of both of these constituent groups, whose combined numbers include nearly all the church-avoiding host population.
Some mnemons are neither memes nor meme-derived in most of their instances. For these mnemons, the study of meme proliferation is of little use. Consider what happens when an earthquake of harmless but noticeable intensity strikes Los Angeles. Millions of people suddenly have the idea that an earthquake has struck on that particular day. So at first the host population does not result primarily from mnemon copying. In fact, the people who directly experience the quake may remain a majority of the idea's hosts, especially if the quake is too mild to get much news coverage. Replicator theory has extremely limited relevance in studying this kind of host population growth. The theory best applies to the limited but still vast realm of memes and meme-derived mnemons, i.e., the realm of memetics.
The ability to unambiguously identify mnemons as HoD now becomes crucial to memetic theory. For instance, when someone receives the hell mnemon from one person and the imminent doomsday mnemon from another, is the resulting A*B combination HoD or HeD? The A*B host has copied both mnemons from pre-existing hosts. But the event that actually forms A*B, namely ~A*B + A*~B --> ~A*B + A*B, does not actually contain A*B as an input mnemon. The mnemon appears not to be distinctly HoD or HeD, a problem in deciding how to proceed.
The problem can be resolved by recalling that mnemons propagate only with respect to an abstraction. Although the A*B host is HoD for abstraction A, and HoD for abstraction B, the instance of A*B is clearly HeD for abstraction A*B. So A*B formed by the event ~A*B + A*~B --> ~A*B + A*B is not a meme, although it is meme-derived.
Yet as mentioned earlier, A*B can also propagate as a set by the proselytic event A*B + ~A*~B --> 2A*B. Formed this way, A*B is a meme. Thus, the host population of A*B is yet another mixture of memes and meme- derived mnemons.
"Meme," Concisely Defined
Defining the word meme concisely but technically without reference to the other neologisms, we have:
MEME. Noun. A memory item, or portion of an organism’s neurally-stored information, identified using the abstraction system of the observer, whose instantiation depended critically on causation by prior instantiation of the same memory item in one or more other organisms’ nervous systems. ("Sameness" of memory items is determined with respect to the above-mentioned abstraction system of the observer.)
Population Psychology and Individual Psychology
In going from individual level considerations to population level considerations, many individual variations statistically cancel to form population level trends in behavior. The same sort of statistical cancellation occurs as when individual molecule velocities collectively form an overall wind velocity. So too do the variations in the magnitude and direction of individual memetic changes largely cancel each other out, along with many variations in individual behavior. The large-scale variations remaining, such as those between host population growth rates, form the basis of evolutionary trends at the population level.
With many self-compounding replication advantages, even a low level trend in mnemon propagating behavior can make a big difference in eventual host population. Still, the memes that accomplish such a trend on a lasting basis tend to be religious taboos, reproductive strictures, political convictions, etc., which have an important impact in the lives of their hosts. Such memes can each have many widespread and lasting effects upon people's lives, including some effects upon meme propagating behavior.
An idea's psychological impact on individual ideological decisions can differ radically from its impact on population ideological decisions. Consider for instance the futuristic decisions to be made about human cloning. Perhaps most people today would say "No, absolutely not!" They might say cloning is "unnatural," "immoral," and "dehumanizing." Of course today, these ideas have no effect on people's reproductive behavior.
All of this might change, however, if human cloning were achieved and became widely affordable. Couples who believed that cloning was good would suddenly have more reproductive options than would couples who thought it was bad. This may very well leave them having more children. They might even typically have four children: two conjugal children and two clones. Moreover, these children (especially the clones) would lean favorably towards accepting and retaining their parents pro-cloning stance. An intense parental propagation advantage would result for the pro-cloning meme. The population might even start evolving a stigma against remaining cloneless. Thus, within only a few generations, the public attitude toward cloning could shift dramatically--and for reasons quite unlike those used by an individual confronted with the issue.
Memetic Evolution is thus a distinct theory of population psychology and does not simply mirror on a magnified scale any theory of individual psychology. Analogously, aerodynamics does not simply mirror on a grand scale the theories of molecular physics.
Memetics does, however, have many specific cases where the population level theory mirrors individual psychology, as with the "God as parent" meme. Here, the wide acceptance of the "God the Father" variety apparently results in part from a subconscious affinity in most individuals for always having a parental figure in their lives. So in this particular case, a feature of population psychology does indeed mirror on large scale a feature of individual psychology.
Propagation advantages of this type may be seen as resulting from an idea being highly adapted to the minds of very many people. Of course, this sort of thinking is not newly arriving with memetics theory. Yet it does fall within a new perspective inside that theory. For instance, the God-as- parent idea can be seen as originating by at least two possible paths: that of being created to fill a psychological need, and that of having been created for some other reason and later proliferating to fill an evolutionary niche formed by the psychological need. The latter possibility might have been realized long ago by a mother who taught her children to think of God as a parent in order to teach them to obey God as one would obey one's parents. The way in which the idea was created does not much matter as long as it has a strong replication advantage to carry it through the population after it has its first host.
Classifying Human Mnemons
Mnemons can be conceptually organized either in terms of what mnemons the people have or what people the mnemons have. To describe change, we can expand these conceptual frameworks: we can say that people acquire mnemons and that mnemons acquire people. The two organizations are merely alternative ways of conceptualizing the same thing--like two alternative coordinate systems for a physics problem.
Yet many mnemon-forming events do not readily suggest a "mnemon acquiring people" perspective. For example, saying that "an electric light idea acquired Thomas Edison" is devoid of any causal meaning; at most it reveals that the idea's set of hosts has just included one more member. (This also is true for the invention of the telephone independently by Edison and Bell, regardless of which one invented it first.) Clearly, Edison got an idea for the electric light, but one cannot meaningfully say that the idea has gotten the person. So the two conceptual frameworks describing the causality of change do not apply equally well in all cases. Nonetheless, each framework can yield distinct insights that are hard to achieve in the other. Analogously, different coordinate systems in physics can be used to gain distinct insights into a single physical process.
Only the homoderivative subset of human mnemons validly admits both the "mnemons acquiring people" and "people acquiring ideas" perspectives. For each HoD mnemon, a pre-existing congeneric instance played a causal role in bringing about the HoD instance. Of course, the person who becomes a mnemon's host plays a causal role in the event too (except for cases of being born with ~A, etc.). So in the HoD sector, both a mnemon and its host play causal roles in pairing up. Within the homoderivative subset of any mnemon's host population, it makes just as much sense to ask how the mnemon "got" a person as to ask how the person "got" the mnemon. Of course, the best way to frame the question varies from idea to idea just as the most useful coordinate system varies from problem to problem in physics. Yet this ability to pick and choose the best way of framing a problem dramatically enhances our ability to gain new understandings.
Actually, the HoD/HeD partition falls slightly short of finding a realm of mnemons where the two conceptual frameworks apply equally well. The reason, it turns out, is that the HoD sector does not guarantee the applicability of the conventional concept of people getting mnemons. Indeed, this conceptual framework does not apply well to the HoD example of the lack-of-birth-control mnemon represented earlier as ~A. It makes sense to say that the ~A mnemon gets new hosts by disposing existing hosts toward having many children. But it makes only dubious sense to say that the new hosts, being born with the ~A-mnemon, actually "get" that mnemon as one would "get" the A-mnemon. So the ideosphere has one subset where only the people-getting-mnemons perspective applies (e.g., new idea creations), another subset where only the mnemons-getting-people perspective applies (lack-of-birth-control mnemon, etc.), and a third, very large subset where both perspectives apply (Amish farming mores, arms racing, etc.)
The main value of partitioning the ideosphere into its homoderivative and heteroderivative sectors is in defining what a self-replicating idea is and what role it plays. The partition accomplishes this partly focusing on the self-replicated idea (HoD mnemon) rather than the self-replicating idea itself. Yet it also does this by telling us how and where in the ideosphere it makes sense to talk about self-replicating ideas. The term "self- replicating idea" characteristically emphasizes one of the two conceptual frameworks, the one that has ideas acquiring people.
The HoD/HeD partition defines the realm of self-propagating ideas, but not the realm of self-preserving ideas. Also, preservational proliferation advantages can apply just as well in the HeD sector as in the HoD sector. For instance, if mnemons A and B have the same HeG formation rate, but A- mnemons last twice as long as B-mnemons, then there will eventually be twice as many HeD A-mnemons as HeD B-mnemons. So in both the HoD and the HeD sector, people can "keep" ideas and ideas can "keep" people. Also, in each sector, the longer a person keeps an idea, the more new people there are likely to be who copy it from her. Yet all these new mnemon copies go to the HoD sector rather than to the HeD sector. So both self-propagation and (hence) self-preservation have a special relationship to the HoD sector.
Qualitative and Quantitative Evolution
As mentioned earlier, occurrence rates of heterogenic events often depend on the prevalence of precursor memes. When vigorous precursor memes proliferate, they achieve substantial odds of causing the creation of memes that only a rare host can form. Additionally, when the new meme is simply defined as a combination of two or more precursor memes, the vigorous propagation of the precursors greatly hastens the arrival of the combination. So the independent spread of meme X and meme Y hastens the formation of the combination X*Y. Indeed, if X and Y spread vigorously, X*Y can pop up explosively among many widely separated individuals. So if X*Y tends to inspire hosts to create mnemon Z, then Z, too can pop up explosively among widely separated individuals. This much acclaimed feature in the innovation of ideas shows that creativity largely a population phenomenon.
Thus, the most vigorous precursor memes tend to recombine with more varieties of new ideas, some of which form an even more vigorously propagating meme package in combination with the precursor set. Mnemon variation thus feeds new operands into the quantitative processes of natural selection while the quantitative processes give many subsequent qualitative variations an appreciable chance to occur. The two kinds of change continuously feed back on each other to form a genuine process of evolution.
Memetic Math
Most examples in this book contain quantitative arguments that must remain tentative, pending the collection of hard data from the population. Expressing these quantitative arguments in ordinary prose can provide impetus for gathering the data, while remaining readable to non-specialists. Ultimately, though, such quantitative reasoning must proceed to the precise and testable language of mathematics. This can assist in understanding what sort of data to collect for testing particular hypotheses. It can also stop scientific disagreements from gravitating to the conclusion that no one can really say anything about thought contagion.
The following two differential equations pertain to two ideas whose host populations are represented by N1(a, t) or N2(a, t)--population age profiles. All members of the total population N(t) are assumed to be counted somewhere in either N1(a, t) or N1(a, t), indicating that the two ideas are complements of each other. (In actual practice, one would often want to divide the population into more subgroups, such as the host populations of an idea, its opposite, and hosts of neither. The present discussion is limited to two groups in order to illustrate quantitative methods as simply as possible.)
The other parameters in the equations have the following meanings: t is time in years, a is host age, p is the age of a second person--the idea propagator--used in places where two people's ages are involved. (Greek letters are spelled out in the HTML text but not in the numbered equations for the online version of this paper.)
R1(a) is the fertility rate for meme 1, in children per host of age a per year--the quantity parental parameter; K11(p, a) is the fraction per year of children of age a who learn meme 1 from an age p parent who hosts meme 1--the efficiency parental rate. K21(p, a) is the fraction per year of children of age a who learn meme 1 from an age p parent who hosts meme 2, a kind of parental "failure rate" for meme 2. Again, for the sake of "simplicity," the different R and K values that may occur when one's parents come from different host populations are not modeled here. (More than just R and K parameters are involved, since the occurrence rates of "mixed" versus "unmixed" couples change with changing host populations.)
gamma12(p, a) is the average annual number of proselytic converts a meme 1 host of age p makes per unit meme 2 host population-age density at age a in his society. beta11(p, a) is the average annual number of proselytic converts a meme 1 host of age p makes per percentage-year of meme 2 hosts of age a in his/her society. Proselytic rates represented by gamma12(p, a) are sensitive to how crowded the society is as a whole while beta12(p, a) rates per meme 1 host are purely sensitive to the fraction of meme 2 hosts in the society. The latter reflects the proselytism between, for instance, spouses: people do not generally double the number of spouses as the population doubles. Yet the number of people one encounters on the street might well double as the population doubles. If so, then proselytic conversations on street corners would be modeled using gamma12(p, a).
alpha1 is the fraction per year of meme 1 hosts who convert to meme 2 without any prior meme 2 hosts teaching them. Preventing such "dropouts" is one form of preservational advantage for meme 1. Finally, M1(a) is the rate of mortality per age a meme 1 host per year.
Swapping "2" subscripts for "1" subscripts in the above sentences gives the parameter definitions corresponding to changes in meme 2 prevalence.
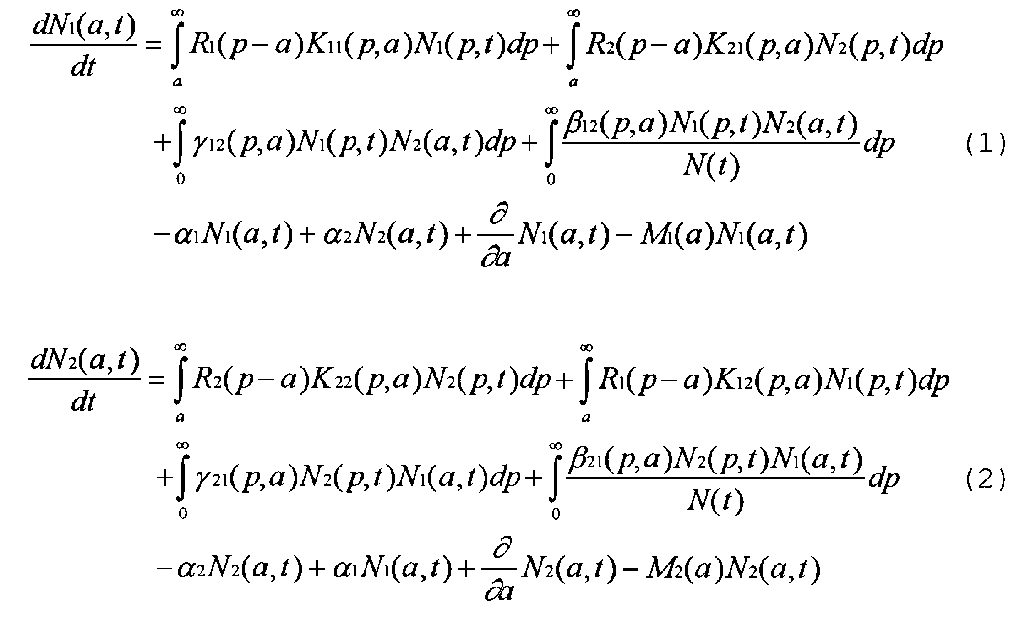
The first two terms in equation 1 are the parental terms. In the first term, the group of N1(p, t) parents of age p is multiplied by the average number R1(p-a) of children per adult that they had a years ago to get the number of children of age a having parents of age p. This then is multiplied by K11(p, a), the fraction per year of children in this latter group having meme 1 passed down to them (while they are of age a and the teaching parent is of age p). This is then integrated over the entire range of parents' ages (p=a) to p=infinity) to get the total rate at which meme 1 hosts are passing the meme down to children of age a. The second term gives the rate at which the meme 2 host population parentally produces meme 1 hosts of age a.
In practice, there may be many cases where a useful mathematical model can be attained by treating the parent to child meme transmission as if it all happened when the children reached the single age c1, the average age at which they pick up meme 1 from a parent. Also, one might find that the transmission rate per child depends very little on parent age differences within the mainstream host childraising years. If this is true, then one can replace the K1(p, a) function with the very simple function k11delta(a-c1), where delta denotes the delta function, and k11 is simply the overall fraction of children who acquire meme 1 from their parents--a much easier thing to measure than transmission versus age. The remaining functions in the parental terms are just fertility versus age and the population age profile--the sort of data that demographers and census-takers have already measured for some groups.
The next two terms in the equation concern the proselytic transmission mode. The first of these is the one that is sensitive to the total number of potential converts, N1(a, t), rather than merely their proportion to the total population. If both N1(a, t) and N2(a, t) doubled, each individual meme 1 host would be winning twice as many converts and the meme 1 host population would be winning four times as many converts per year. On the other hand, the second term on line two would only double, and not quadruple, if each group doubled. In reality, the dependence of proselytic conversation rates on host population sizes is more complicated than the two terms suggest, and the nature of the dependency would need to be studied empirically as part of any mathematical modeling effort for memes with significant proselytic transmission. As with the parental terms, the proselytic terms may be simplified in some cases by replacing the age dependencies with "lumped" effective propagations at certain effective ages.
The following two terms (beginning of line 3) express the "spontaneous" dropout rate for meme 1 and meme 2, respectively. "Spontaneous" dropout rates are assumed to be proportional simply to the number of hosts capable of dropping out.
The next term is the partial derivative of N1(a, t) with respect to a. This term indicates that part of the changing population age profile of meme 1 is due to simple aging of its host population.
The final term expresses the mortality rate as a function of age among meme 1 hosts. Mortality per host per year at age a (a kind of actuarial data) is simply multiplied by the number of hosts at age a to give the overall rate.
Equation 2 above models the same kinds of propagation processes for meme 2 as are modeled for meme 1. Equations 1 and 2 form a system of non-linear differential equations modeling the interdependent propagation of meme 1 and meme 2.
What follows are five more equations that go with equations 1 and 2, defining relationships between the propagation parameters. Equation 3 states that all offspring of meme 1 parents end up holding either meme 1 or meme 2. Equation 4 says the same thing for meme 2 parents. Equations 5 and 6 state that one group's proselytic gains are the other group's proselytic losses, so that the net proselytic gain to the whole population is 0. The last equation merely defines the function N1(t), the total population versus time, as the sum of the as the sum of the two meme host populations, all ages included.
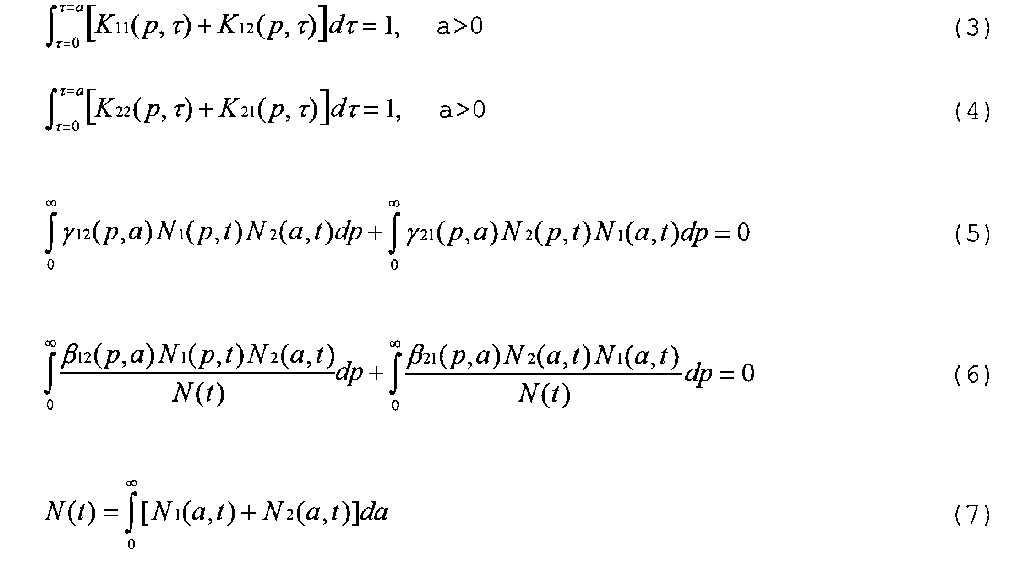
Not all meme propagation events are given their own separate terms in equations 1 and 2. For instance, if it frequently happened that meme 1 hosts produced meme 2 offspring who then converted their parents to meme 2, then the rate at which meme 1 hosts were proselytically converted to meme 2 might depend greatly on how many children they had. A new term might have to be added to the equations to make this phenomenon adequately modeled. The model can, in fact, be made arbitrarily complex, but it is obviously desirable to keep it as simple as the application permits.
Another elaboration of the equations, and one that might interest mathematical sociobiologists, is the explicit inclusion of specific genes and their propagation parameters into the picture. Such a model would analyze "host populations" of ideas, genes, and idea-gene combinations all in the same system of equations. Of course, one sets the alpha's, beta's, and gamma's to zero wherever the propagation of a gene is modeled. The parental terms become more numerous and take on a diversity of forms corresponding to all the combinations of genes and memes that can occur in two mating adults. Each possible outcome of each parent combination must have its own term in one of the equations. Such equations embody no a priori assertions about the relative importance of either genetic change or cultural change over a modeled time span, nor any assertions of how strongly or weakly prior genetic and cultural evolution constrains the course of change over that time span. Instead, they allow for considering these matters on a case by case basis once the requisite starting data are fed into the models.
Although motivational and cognitive factors are not readily conspicuous in equations 1 and 2, they are in fact represented. The reason is the K's, beta's, and gamma's are measures of successful meme transfer events. As such, they are composites of both the rates at which propagation is attempted and the rates at which it is cognitively and motivationally well-received. Likewise, the "spontaneous" dropout rates (alpha's) include their own products of cognition and motivation.
Anti-competitor propagation advantage, on the other hand, is not fully represented by the K's, beta's, and gamma's. Part of the reason is that this mode can occur in quite a wide range of ways. It makes a big difference, for instance, whether the meme 1 group merely bans meme 2 proselytizing or launches a meme 2 extermination campaign. Moreover, the effectiveness of such measures does not vary as a simple function of the meme host populations. The Nazis, for instance, became dramatically more harmful to competitors after they became numerous enough to gain political power. Such phenomena may well defy mathematical modeling techniques aimed at predicting host populations versus time.
Equations 1 and 2 are not offered to model anything but fairly ideal cases of the two-idea propagation problem. They do, however, offer a sample of the kinds of terms that can arise in realistic applications, and they illustrate that a unified quantitative analysis can be given to qualitatively dissimilar modes of propagation. They also illustrate the concept that once the main mechanisms of an idea's propagation have been empirically discovered and measured, the degree to which each mechanism contributes to instantaneous rates of propagation can be mathematically modeled. The resulting systems of differential equations govern host populations as a function of time, and so can be used to generate limited predictions of what will happen if the equation parameters remain reasonably constant in non-chaotic intervals.
Alternatively, one can use the quantified propagation mechanisms to run predictive computer simulations of memetic evolution without the intermediate step of writing down differential equations. The latter method might run particularly well on systems based on "cellular automata," where each "cell" simulates the memetic state and behavior of a person.
Acknowledgments
My gratitude goes to Carl Wegner for his great generosity in funding this work.
I also thank Curt Hicks and Michael Crowley for their comments and work on earlier drafts of this paper.
BIBLIOGRAPHY
Bonner, John Tyler 1980. The Evolution of Culture in Animals. Princeton: Princeton University Press
Boyd, Robert, and Richerson, Peter J. 1985. Culture and the Evolutionary Process. Chicago: University of Chicago Press.
Cloak, F. T. 1975. "Is a Cultural Ethology Possible?", Human Ecology, 3, pp. 161-182.
Dawkins, Richard 1976. The Selfish Gene. Oxford: Oxford University Press.
Drexler, K. Eric 1987. Engines of Creation. New York: Anchor Press/Doubleday.
Gleick, James 1987. Chaos: Making a New Science. New York: Viking Penguin Inc.Grmek,
Hofstadter, Douglas R. and Dennett, Daniel C. 1981: The Mind's I. New York: Basic Books.
Hofstadter, Douglas R. 1980. Gödel, Escher, Bach: an Eternal Golden Braid. New York: Basic Books.
-------. 1985. Metamagical Themas: Questing for the Essence of Mind and Pattern. New York: Basic Books.
Lumsden, Charles J. and Wilson, Edward O. 1981. Genes, Mind, and Culture. Cambridge: Harvard University Press.
Lynch, Aaron 1996. Thought Contagion. New York: Basic Books. In process.
Rogers, Everett M. 1983. The Diffusion of Innovations.
New York: The Free Press.